Context Parallelism
As you can see, Large Language Model is taking over the world, everyone is using it, and it able to augment humanity productivity and intelligence beyond what we expect.
You can chat with the LLM to do practically everything you want, from roleplaying as a baby up to asking feedback loops for research papers that you do not understand.
During ChatGPT released on November 30, 2022, it only support max 4096 context length or 4096 tokens, 1 token average 2 words based on ChatGPT tokenizer, so 8192 words. Let use chat bubbles below as an example, green chat bubbles is the user while gray chat bubbles is the assistant,
For this example, let us assume 1 token equal to 1 word, so the words are ['hello', 'hi!', 'How', 'can', 'I', 'help', 'you?', 'do', 'u', 'know', 'about', 'Malaysia?', 'Of', 'course', 'I', 'know', 'about', 'Malaysia!'], 18 words or 18 tokens. So when we say the LLM support 4096 context length, it can support multi-turn conversation will the total 4096 tokens.
Today, LLM can support million tokens of context length, Gemini from Google can support up to 1 million tokens of context length, you can give an entire book or research paper and ask any question that you want!
From 4096 context length up to 1 million context length in less than 2 years!
How does LLM able to serve from just 4096 tokens to become 1 million tokens? Context Parallelism!
But before that, we need to know the memory usage of Attention mechanism.
Attention is all you need!
And Attention mechanism defined as,
Where `Q` is query matrix, `K` is key matrix, and `V` is value matrix. LLM is decoder model so the attention happened is self-attention. Now for an example, ,
- Hidden size or `d_model` for QKV is 10, so QKV with each size [2, 10], 2 input dimension, 10 hidden dimension.
- the input shape is [5, 2], 5 sequence length or `L`, 2 hidden dimension or `in_d_model`.
- Input will matmul with QKV matrices,
- 1. input [5,2] matmul Q [2, 10] = [5, 10]
- 2. input [5,2] matmul K [2, 10] = [5, 10]
- 3. input [5,2] matmul V [2, 10] = [5, 10]
- 4. After that calculate Attention,
The output shape should be [Q `L`, V `d_model`] = [5, 10]. To calculate the memory usage roughly based on output shape,
- 1. Q, K and V linear weights, which each output is [in_d_model, d_model], 3 x in_d_model x d_model.
- 2. input matmul Q, K and V, which each output is [L, d_model], 3 x L x d_model.
- 3. softmax(QK^T)V, [L, d_model], L x d_model.
- 4. Total, (3 x in_d_model x d_model) + (3 x L x d_model) + (L x d_model) = 260.
- 7. Assumed we store in bfloat16, 260 x 2 = 520 bytes.
520 bytes is super small and yes that is for a simple example, but what if we use at least LLM 8B parameters such as Llama 3.1?
Use actual Llama 3.1 8B parameters
Based on the Llama 3.1 8B parameters settings from HuggingFace, https://huggingface.co/meta-llama/Meta-Llama-3.1-8B/blob/main/config.json, there are 3 settings important for attention size,
- 1. `hidden_size` = 4096.
- 2. `num_attention_heads` = 32.
Because Llama use multi-head attention and to simplify the attention, assumed no group multi-head attention been used aka `num_key_value_heads`, assume the input shape is [5, 4096], 5 sequence length with 4096 hidden size, so during calculating the attention,
- 1. `head_dim` = hidden_size // num_attention_heads
- 2. Q, K, V linear weights [hidden_size, num_attention_heads x head_dim], 3 x hidden_size x num_attention_heads x head_dim.
- 3. input matmul Q, K and V, which each output is [L, num_attention_heads x head_dim] and reshape become [num_attention_heads, L, head_dim], 3 x L x num_attention_heads x head_dim.
- 4. softmax(QK^T)V = [num_attention_heads, L, head_dim], num_attention_heads x L x head_dim.
- 5. Total, (3 x hidden_size x num_attention_heads x head_dim) + (3 x L x num_attention_heads x head_dim) + (num_attention_heads x L x head_dim) = 50413568.
- 6. Assumed we store in bfloat16, 50413568 x 2 = 100827136 bytes or 0.100827136 GB, still small.
Now what if you got 1M sequence length or 1M context length? replace the `L` with 1M, you got 16434331648 bytes, saved as bfloat16, 16434331648 x 2 = 32868663296 bytes or 32.868663296 GB!
32.868663296 GB just for the attention, not included other linear layers and other matmul operations, insane. How about 13B or 70B parameters? kebabom!
Context Parallelism
When we talk about Parallelism in deep learning, it is about how to parallelize the data into multiple GPUs either to reduce computation burden and at the same reduce memory consumption or replicating the replica to increase the size of input to make learning process faster, and Context Parallelism is about how to parallelize the sequence length into multiple GPUs. Let say I have 2 GPUs, so the partition size is 2,
So now each GPUs can calculate their own local attention but still coherent with the other local attentions and if you gather and combine the local attentions, the combined should be almost the same with the full attention with super super small different, and you save GPU memory is saved by a factor of partition size!
If we split the QKV into 2 GPUs, Q = [Q1, Q2], K = [K1, K2], V = [V1, V2], so local attentions, Attention1=softmax(Q1K1^T)V1 and Attention2=softmax(Q2K2^T)V2.
Now, how does softmax(Q1K1^T)V1 able to correlate with softmax(Q2K2^T)V2 ? Especially on softmax, because softmax required sum of exponents on the hidden dimension.
Blockwise Parallel Transformer for Large Context Models
This paper Blockwise Parallel Transformer for Large Context Models: 2305.19370 shows that we can calculate Attention in blockwise manner on multiple devices.
And this paper also mentioned `Self-attention can be computed in a blockwise manner without materializing the softmax attention matrix` which already done from Flash Attention: 2205.14135 and Self-attention does not need o(n2) memory: 2112.05682
Flash Attention
Flash Attention: 2205.14135 partitioned QKV into blocks inside the GPU and write in CUDA kernel and optimized the movement between GPU high bandwidth memory (HBM) and GPU on-chip SRAM, become more "io-awareness" by directly manipulating the memory hierarchy using CUDA interface. Flash Attention also calculate the attention using blockwise manner inside CUDA blocks.
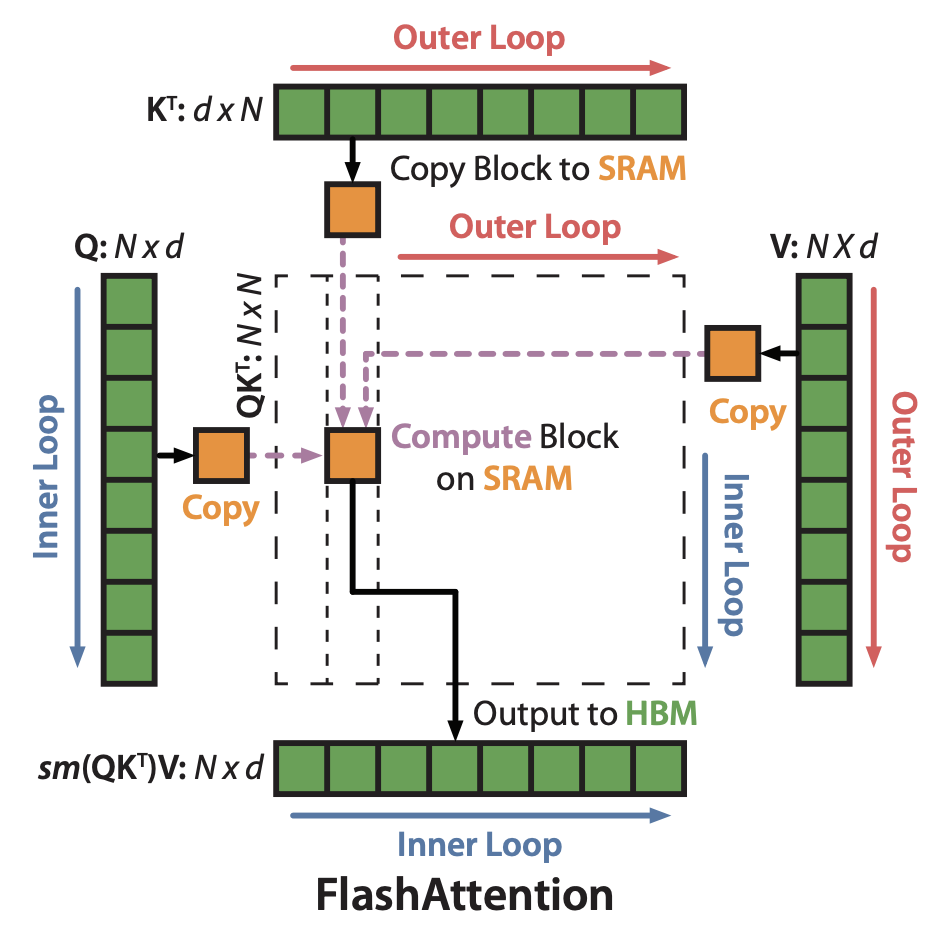

- As you can see there are outer and inner loops, defined as, loop for each KV blocks, nested loop for each Q blocks, and calculate local max and local attention, gather local max to get global max and for each local attention minus with global max to get the global attention.
Self-attention does not need o(n2) memory
While Self-attention does not need o(n2) memory: 2112.05682 write using Jax to compute the blockwise, it is not as efficient as Flash Attention: 2205.14135 because Jax handled all the memories and there is no interface to make it "io-awareness" like Flash Attention: 2205.14135. The implementation,
```python
import functools, jax, math
from jax import lax
from jax import numpy as jnp
def _query_chunk_attention(query,
key,
value,
key_chunk_size=4096,
precision=lax.Precision.HIGHEST,
dtype=jnp.float32):
num_kv, num_heads, k_features = key.shape
v_features = value.shape[-1]
key_chunk_size = min(key_chunk_size, num_kv)
query = query / jnp.sqrt(k_features).astype(dtype)
@functools.partial(jax.checkpoint, prevent_cse=False)
def summarize_chunk(query, key, value):
attn_weights = jnp.einsum(
'qhd,khd->qhk', query, key, precision=precision).astype(dtype)
max_score = jnp.max(attn_weights, axis=-1, keepdims=True)
max_score = jax.lax.stop_gradient(max_score)
exp_weights = jnp.exp(attn_weights - max_score)
exp_values = jnp.einsum(
'vhf,qhv->qhf', value, exp_weights, precision=precision).astype(dtype)
return (exp_values, exp_weights.sum(axis=-1),
max_score.reshape((query.shape[0], num_heads)))
def chunk_scanner(chunk_idx):
key_chunk = lax.dynamic_slice(
key, (chunk_idx, 0, 0),
slice_sizes=(key_chunk_size, num_heads, k_features))
value_chunk = lax.dynamic_slice(
value, (chunk_idx, 0, 0),
slice_sizes=(key_chunk_size, num_heads, v_features))
return summarize_chunk(query, key_chunk, value_chunk)
chunk_values, chunk_weights, chunk_max = lax.map(
chunk_scanner, xs=jnp.arange(0, num_kv, key_chunk_size))
global_max = jnp.max(chunk_max, axis=0, keepdims=True)
max_diffs = jnp.exp(chunk_max - global_max)
chunk_values *= jnp.expand_dims(max_diffs, axis=-1)
chunk_weights *= max_diffs
all_values = chunk_values.sum(axis=0)
all_weights = jnp.expand_dims(chunk_weights, -1).sum(axis=0)
return all_values / all_weights
def mefficient_attention(query,
key,
value,
query_chunk_size=1024,
precision=jax.lax.Precision.HIGHEST,
dtype=jnp.float32):
num_q, num_heads, q_features = query.shape
def chunk_scanner(chunk_idx, _):
query_chunk = lax.dynamic_slice(
query, (chunk_idx, 0, 0),
slice_sizes=(min(query_chunk_size, num_q), num_heads, q_features))
return (chunk_idx + query_chunk_size,
_query_chunk_attention(
query_chunk, key, value, precision=precision, dtype=dtype))
_, res = lax.scan(
chunk_scanner,
init=0,
xs=None,
length=math.ceil(num_q / query_chunk_size))
return res.reshape(num_q, num_heads, value.shape[-1])
```
- But basically is the same, loop Q blocks, loop nested KV blocks, and calculate local max and local attention, gather local max to get global max and for each local attention minus with global max to get the global attention.
-- i. Chunk Q into blocks,
```python
query_chunk = lax.dynamic_slice(
query, (chunk_idx, 0, 0),
slice_sizes=(min(query_chunk_size, num_q), num_heads, q_features))
```
-- ii. Calculate QiKj^T,
```python
attn_weights = jnp.einsum('qhd,khd->qhk', query, key, precision=precision).astype(dtype)
```
-- iii. Calculate local max,
```python max_score = jnp.max(attn_weights, axis=-1, keepdims=True) ```
-- iv. Calculate blockwise Attention,
```python global_max = jnp.max(chunk_max, axis=0, keepdims=True) max_diffs = jnp.exp(chunk_max - global_max) chunk_values *= jnp.expand_dims(max_diffs, axis=-1) chunk_weights *= max_diffs all_values = chunk_values.sum(axis=0) all_weights = jnp.expand_dims(chunk_weights, -1).sum(axis=0) all_values / all_weights ```
But Flash Attention: 2205.14135 and Self-attention does not need o(n2) memory: 2112.05682 partitioned the QKV into blocks happened inside a single GPU, not for multi-GPUs.
And actually, Blockwise Parallel Transformer for Large Context Models: 2305.19370 take inspiration directly from Self-attention does not need o(n2) memory: 2112.05682, but just do it on multi-GPUs level.
Blockwise Parallel Transformer for Large Context Models, Section 3
In section 3, it stated Q can split into Bq blocks, and KV split into Bkv blocks, same as Flash Attention: 2205.14135 and Self-attention does not need o(n2) memory: 2112.05682.
- 1. For each query block, the blockwise attention Attention(Qi, Kj, Vj) can be computed by iterating over all key-value blocks,
- 2. The scaling operation scales each blockwise attention based on the difference between the blockwise maximum and the global maximum.
- 3. Once the blockwise attention is computed, the global attention matrix can be obtained by scaling the blockwise attention using the difference between the blockwise and global softmax normalization constants.
- 4. But I believe there is a mistake to calculate \(\mathrm{Attention}(Q_i, K, V)\),
-- i. \(Q_i K_j^T\) shape is [L, L] while \(\mathrm{Attention}(Q_i, K, V)\) shape is [L, dim], so we cannot do hadamard product.
-- ii. It should be \(\exp(\max(Q_i K_j^T) - \mathrm{max}_i)\), so the shape will become [L]. When we do hadamard product, [L] o [L, dim], PyTorch will automatically repeat [L], [L, L, ...] become [L, dim] then we can do [L, dim] o [L, dim].
--- iii. Actual equation should be,
Visualization to get for Attention(Qi, K, V),
- 1. For Qi, loop for each KV blocks, j,
-- i. Calculate maxj = max(QiKj^T) and Attentionj = softmax(QiKj^T - maxj)Vj
-- ii. Store maxj in maxi, maxi = [maxj0, maxj1, ...] and Attentionj in Attentioni, Attentioni = [Attentionj0, Attentionj1, ...]
- 2. Calculate max_maxi = max(maxi), loop again KV blocks, j,
-- i. Calculate blockwisej = exp(maxj - max_maxi) x Attentionj, and store it in blockwisei, blockwisei = [blockwisej0, blockwisej1, ...]
-- ii. Sum blockwisei, now you got Attention(Qi,K,V)!
PyTorch code using Loop
To test if it is working, we have to compare by doing full attention vs blockwise attention, after that we compare the full attention on the first partition size with the first blockwise attention,
```python
import torch
import torch.nn.functional as F
Q = torch.randn(100, 128).cuda().to(torch.bfloat16)
K = torch.randn(100, 128).cuda().to(torch.bfloat16)
V = torch.randn(100, 128).cuda().to(torch.bfloat16)
full_attention = torch.matmul(F.softmax(torch.matmul(Q, K.T), dim = -1), V)
chunk_size = 2
Q_blocks = torch.chunk(Q, chunk_size)
K_blocks = torch.chunk(K, chunk_size)
V_blocks = torch.chunk(V, chunk_size)
Q_block = Q_blocks[0]
block_attentions = []
block_maxes = []
for K_block, V_block in zip(K_blocks, V_blocks):
# Compute attention scores
scores = torch.matmul(Q_block, K_block.T)
# Compute block-wise max
block_max = scores.max(dim=-1, keepdim=True)[0]
block_maxes.append(block_max)
# Compute block-wise attention
block_attention = torch.matmul(F.softmax(scores - block_max, dim=-1), V_block)
block_attentions.append(block_attention)
# Compute global max
global_max = torch.max(torch.cat(block_maxes, dim=-1), dim=-1, keepdim=True)[0]
# Scale and combine block attentions
scaled_attentions = [
torch.exp(block_max - global_max) * block_attention
for block_max, block_attention in zip(block_maxes, block_attentions)
]
output = sum(scaled_attentions)
```
Exact match signs,
```python (torch.sign(full_attention[:output.shape[0]]) == torch.sign(output)).float().mean() ```
The output,
```text tensor(0.9958, device='cuda:0') ```
Check different on `argmax(-1)`,
```python print(full_attention[:output.shape[0]].argmax(-1), output.argmax(-1)) ```
Output,
```text
tensor([122, 84, 27, 20, 98, 60, 36, 65, 39, 48, 31, 91, 48, 69,
80, 98, 59, 121, 0, 24, 42, 67, 76, 58, 36, 34, 79, 1,
57, 99, 9, 47, 77, 110, 9, 9, 119, 9, 34, 27, 6, 37,
104, 121, 103, 123, 0, 56, 67, 104], device='cuda:0')
tensor([122, 84, 27, 20, 98, 60, 36, 65, 39, 48, 31, 91, 48, 69,
80, 98, 59, 121, 0, 24, 42, 39, 76, 58, 36, 34, 79, 1,
57, 40, 9, 47, 77, 110, 9, 9, 119, 9, 34, 27, 6, 37,
104, 121, 103, 123, 0, 56, 67, 104], device='cuda:0')
```
You can continue to run for Q blocks or Bq blocks. As you can see, this blockwise is exactly as Self-attention does not need o(n2) memory: 2112.05682, just in PyTorch.
Use PyTorch distributed
Now we have to convert from loop execution to parallel execution using Torch Elastic Distributed, for me, if you want to do parallel execution, at first you must test it using loop execution, if it works, convert it to parallel execution.
```python
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.distributed as dist
import os
def main():
world_size = torch.cuda.device_count()
local_rank = int(os.environ["LOCAL_RANK"])
device = f'cuda:{local_rank}'
dist.init_process_group(backend='nccl')
Q_block = torch.randn(50, 128).cuda(device=device).to(torch.bfloat16)
K = torch.randn(50, 128).cuda(device=device).to(torch.bfloat16)
V = torch.randn(50, 128).cuda(device=device).to(torch.bfloat16)
block_attentions = []
block_maxes = []
for i in range(world_size):
if i == local_rank:
dist.broadcast(K, src=i)
dist.broadcast(V, src=i)
K_block = K
V_block = V
else:
K_block = torch.empty_like(K)
V_block = torch.empty_like(V)
dist.broadcast(K_block, src=i)
dist.broadcast(V_block, src=i)
scores = torch.matmul(Q_block, K_block.T)
block_max = scores.max(dim=-1, keepdim=True)[0]
block_maxes.append(block_max)
block_attention = torch.matmul(F.softmax(scores - block_max, dim=-1), V_block)
block_attentions.append(block_attention)
global_max = torch.max(torch.cat(block_maxes, dim=-1), dim=-1, keepdim=True)[0]
scaled_attentions = [
torch.exp(block_max - global_max) * block_attention
for block_max, block_attention in zip(block_maxes, block_attentions)
]
output = sum(scaled_attentions)
print(local_rank, len(block_maxes), output.shape)
if __name__ == "__main__":
main()
```
Save it as `context-parallelism.py`, and this example required minimum 2 GPUs, and to execute it using `torchrun`,
```bash torchrun \ --nproc-per-node=2 \ context-parallelism.py ```
The output,
``` 0 2 torch.Size([50, 128]) 1 2 torch.Size([50, 128]) ```
For each GPU able to get expected shape which is [50, 128], so the data flow is like,
- 1. When we do context parallelism, each QKV blocks already initialized for each GPU, not during GPU 0 after that split to N GPUs, because GPU 0 it self not enough memory to chunks and scatter to N GPUs.
- 2. We loop based on world size, if we got 2 GPUs, so the world size 2. If,
-- i. If i equal to current device, `i == local_rank`, we have to broadcast KV blocks to other GPUs.
-- ii. If i does not equal to current device, it means the local GPU must accept KV blocks from the other GPUs.
-- iii. Calculate max(QiKj^T) and store it in block_maxes.
-- iv. Calculate softmax(QiKj^T - max(QiKj^T))Vj and store it in block_attentions.
- 3. Calculate the global_max from block_maxes.
- 4. We iterate for each blocks from zip(block_maxes, block_attentions),
-- i. Calculate exp(block_max - global_max) * block_attention and store in scaled_attentions.
- 5. Sum scaled_attentions to get the blockwise attention at local GPU.
- 6. The data movement is like below,
Improvement
Ring Attention: 2310.01889 from the same authors to improve this Blockwise Attention by simply reduce the communication between nodes by using ring communication.
And recently there is Tree Attention: 2408.04093 to improve Ring Attention by aggregating the max(KV.T) on tree hierarchy, which is only make sense for multi-nodes.